다익스트라(Dijkstra) 알고리즘

인터넷정보

다익스트라(Dijkstra) 알고리즘

알 수 없는 사용자 2007. 10. 17. 18:04

다익스트라(Dijkstra) 알고리즘
 다익스트라(Dijkstra) 알고리즘은 최단거리를 구하는 방법으로 유명한 알고리즘입니다. 
이 방법은 그리디하면서 다이나믹한 방법입니다.(뭔말이지? --;) 
먼저 그리디적이라는 말은 현시점에서 볼 때 자신과 
연결된 곳 중 가장 짧은 곳을 찾는다는 것이고, 다이나믹하다는 말은 시발점에서 
어떤 점까지의 거리를 저장해 둬서 그 저장해 둔 거리를 이용해서 더 먼 곳까지의 
최단거리를 구하기 때문입니다.(결국엔 다이나믹이군..) 
사실 이렇게 말로만 들어서는 뭘 어떻게 해야할지 감이 잘 안 오실겁니다. 
이제 다익스트라 알고리즘에 대해서 자세히 알아보죠.


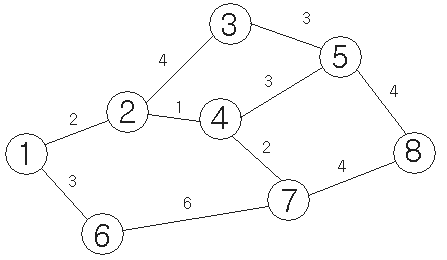
 위와 같은 그래프가 있다고 합시다. 그럼 이 그래프를 가지고 1에서 8로 가는 
최단거리를 다익스트라를 이용해서 구해 보겠습니다.
 먼저, 이 그래프를 인접행렬로 나타냅니다.
0 2 m m m 3 m m
2 0 4 1 m m m m
m 4 0 m m 3 m m
m 1 m 0 3 m 2 m
m m 3 3 0 m m 4
3 m m m m 0 6 m
m m m 2 m 6 0 4
m m m m 4 m 4 0여기서 m값은 충분히 큰 값을 의미하는 상수입니다. 
충분히 큰 값이란 말은 "너무 멀어서 이동할 수 없다."라는 뜻이고, 다른 값들보다 
더 크기만 하면 됩니다. integer형이면 대충 30000만정도로 주면 됩니다. 
32767을 주면 안됩니다. 궁금하시면 직접 해보세요. 어떻게 되나.. 
정확한 범위는 (최단거리<m<=가장 큰 값(integer에선 32767)-최단거리) 
 1과 연결된 모든 정점 중 최소값을 가진 정점(여기서는 2) 에 표시를 붙여 확정합니다. 
그 확정한 정점과 연결된 정점사이의 거리를 구하고, 아직 표시를 하지 않은 정점의 거리 중 
최소값을 가진 정점에 표시를 붙여 확정합니다. 이런 식으로 모든 정점에 표시가 
붙여 확정하면 1에서 어디로 가는 최단거리도 다 구할 수 있습니다. 정리하면 다음과 같습니다.
1. 시작점과 연결된 정점 중 최소값을 가진 정점에 표시를 붙여 확정한다.

2. 확정한 정점과 연결된 모든 정점의 거리를 구해서 저장해 둔다.

3. 모든 정점에 표시가 붙어 확정될 때까지 반복한다.

program dijkstra;
 const
 n=8;
 m=5000;
 data:array[1..n,1..n] of integer= (
 (0,2,m,m,m,3,m,m),
 (2,0,4,1,m,m,m,m),
 (m,4,0,m,m,m,3,m),
 (m,1,m,0,3,m,2,m),
 (m,m,3,3,0,m,m,4),
 (3,m,m,m,m,0,6,m),
 (m,m,m,2,m,6,0,4),
 (m,m,m,m,4,m,4,0));
 var
 i,j,k,s,e,min: integer; {s는 시작점, e는 끝점, min은 거리의 최소값}
 v,distance:array[1..n] of integer; {v는 확정표시, distance[i]는 시작점에서 i까지의 최단 거리}
 begin
 write('시작점을 입력하시오 : ');readln(s);
 write('도착점을 입력하시오 : ');readln(e);
 
 for j:=1 to n do
 begin
 v[j]:=0; {방문상태 초기화}
 distance[j]:=m; {거리를 전부 최대값을 넣음}
 end;
 
 distance[s]:=0; {자신에서 자신까지의 거리는 0이므로..}

 for i:=1 to n do
 begin
 min:=m;
 for j:=1 to n do {연결된 곳 중 최단거리인 곳을 찾음}
 if (v[j]=0) and (distance[j]<min) then 
 begin
 k:=j;
 min:=distance[j];
 end;
	
 v[k]:=1; {연결된 곳 중 최단거리인 곳을 확정}
 
 if min=m then {min=m은 위에 루프에서 if의 조건을 만족한 적이 한번도 없다는 말}
 begin {즉,연결된 곳이 아예 없다는 말과도 같다.} 
 write('연결되어 있지 않습니다.'); 
 exit;
 end;

 for j:=1 to n do
 if distance[k]+data[k,j] < distance[j] then {s->k->j의 거리 < s->j의 거리}
 distance[j]:=distance[k]+data[k,j]; {그 값(s->k->j의 거리)을 j로 가는 최단거리로 저장}
 end;
 writeln(s,'=>',e,':',distance[e]);
 end.

한번만 봐서는 이해가 잘 안 되실 수도 있습니다. (뭐.. 머리가 좋으신 분이시라면.. 그렇지도 않겠지만..) 잘 이해가 안 되시면 그래프를 가지고 그림을 그려보세요. 그럼 이해하는데 많은 도움이 될 것입니다.

이상으로 다익스트라 알고리즘 강좌를 마칩니다. 질문 있는 분은 Q&A게시판에 글 남겨주세요. 다음은 모든 정점을 출발점으로 하는 플로이드(Floyd)알고리즘에 대한 강좌를 하겠습니다. 그럼 오늘도 즐플~^^;

http://yalli.new21.org/or_algorithm/algorithm/graph/dijkstra.htm

다른 참고 소스입니다. (phpschool)

#include <stdio.h>
#define MAX 100

int n,m,board[MAX+1][MAX+1],start,end,object;
int check[MAX+1],point[MAX+1],path[MAX+1],pass[MAX+1];

void in();
void sol();
void out();

void main()
{
in();
sol();
out();
}

void in()
{
int i,p,q,w;
FILE *fi = fopen("short.inp","r");
fscanf(fi,"%d",&n);
fscanf(fi,"%d",&m);
for (i=1;i<=m;i++)
{
fscanf(fi,"%d %d %d",&p,&q,&w);
board[p][q]=w;
board[q][p]=w;
}
fscanf(fi,"%d %d",&start,&end);
fclose(fi);
}

void sol()
{
int i,j,s,max;
point[start]=0;
s=start;
for (i=1;i<n;i++)
{
for (j=1;j<=n;j++)
{
if (j==start)
continue;
if (board[s][j] > 0 &&(point[j] == 0 || point[j] > point[s]+board[s][j] ))
{
point[j]=point[s]+board[s][j];
path[j]=s;
}
}
if (end==s)
break;
check[s]=1;
max=32767;
for (j=1;j<=n;j++)
if (check[j]==0 && max > point[j] && point[j]!=0)
{
max=point[j];
s=j;
}
}
object =point[end];
s=end;
i=2;
pass[1]=end;
while(s!=start)
{
pass[i]=path[s];
s=path[s];
i++;
}
pass[0]=i-1;
}

void out()
{
int i;
FILE *fo;
fo = fopen("short.out","w");
fprintf(fo,"%d\n",object);
for (i=pass[0];i>1;i--)
fprintf(fo,"%d %d\n",pass[i],pass[i-1]);
fclose(fo);
}

지하철 역간 최단 거리 검색 프로그램을 만들어 보려고 검색하다보니
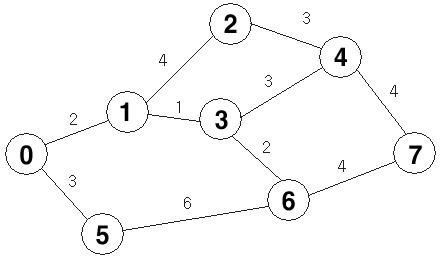
유명한 알고리즘 중 다익스트라 알고리즘이라는 걸 알게 되었습니다.
소스는 델파이와 C로 된거 밖에 없어서, 해당 소스를 PHP 버전으로 바꿔봤습니다.
참고하세요.

<?php
$n=8;
$m=5000;
$data = array();
$data[] = array(0,2,$m,$m,$m,3,$m,$m);
$data[] = array(2,0,4,1,$m,$m,$m,$m);
$data[] = array($m,4,0,$m,$m,$m,3,$m);
$data[] = array($m,1,$m,0,3,$m,2,$m);
$data[] = array($m,$m,3,3,0,$m,$m,4);
$data[] = array(3,$m,$m,$m,$m,0,6,$m);
$data[] = array($m,$m,$m,2,$m,6,0,4);
$data[] = array($m,$m,$m,$m,4,$m,4,0);
$distance = array();
$v = array();
$s = 0; // 시작점
$e = 7; // 끝점
for($j=0; $j < $n; $j++)
{
$v[$j] = 0;
$distance[$j] = $m;
}
$distance[$s] = 0;
for($i=0; $i< $n; $i++)
{
$min = $m;
for($j=0; $j < $n; $j++)
{
if(($v[$j] == 0) && ($distance[$j] < $min))
{
$k = $j;
$min = $distance[$j];
}
}
$v[$k] = 1;
if($min == $m)
{
print '연결되어 있지 않습니다.';
exit;
}
for($j = 0 ; $j < $n; $j++)
{
if($distance[$k]+$data[$k][$j] < $distance[$j])
{
$distance[$j] = $distance[$k] + $data[$k][$j];
}
}
}
print $s." = ".$e." : ".$distance[$e];
?>

** 플로이드 알고리즘 : 최단거리검색 **
참고로 해당 알고리즘은 A, B 지점까지의 최단 거리를 구할 수 있습니다.
위 알고리즘을 응용하면, 해당 최단 거리의 경로도 구할 수 있습니다.

<?php
$n=8;
$m=5000;
$a = array();
$a[] = array(0,2,$m,$m,$m,3,$m,$m);
$a[] = array(2,0,4,1,$m,$m,$m,$m);
$a[] = array($m,4,0,$m,$m,$m,3,$m);
$a[] = array($m,1,$m,0,3,$m,2,$m);
$a[] = array($m,$m,3,3,0,$m,$m,4);
$a[] = array(3,$m,$m,$m,$m,0,6,$m);
$a[] = array($m,$m,$m,2,$m,6,0,4);
$a[] = array($m,$m,$m,$m,4,$m,4,0);
for($k = 0; $k < $n; $k++){
for($i = 0; $i < $n; $i++){
for($j = 0; $j < $n; $j++){
if ($a[$i][$j] > $a[$i][$k] + $a[$k][$j]) { $a[$i][$j] = $a[$i][$k] + $a[$k][$j]; }
}
}
}
for($i = 0; $i < $n; $i++){
for($j = 0; $j < $n; $j++){
print $i . "=>". $j ." : " . $a[$i][$j];
print "<br />";
}
}
?>

'인터넷정보' 카테고리의 다른 글

자바스크립트 :: 객체 prototype에서 setInterval 문제점 (0)	2007.10.17
자바스크립트 :: 객체 prototype에서 setInterval 문제점 (0)	2007.10.17
자바스크립트 배열 검사 (0)	2007.10.17
자바스크립트 배열 검사 (0)	2007.10.17
다익스트라(Dijkstra) 알고리즘 (0)	2007.10.17
TV, 영화에 사용된 폰트 (0)	2007.10.17
TV, 영화에 사용된 폰트 (0)	2007.10.17
키보드 눌러서 새창띄우기 (0)	2007.10.17
키보드 눌러서 새창띄우기 (0)	2007.10.17
페이지 이동 스크립트 (0)	2007.10.17

현재글다익스트라(Dijkstra) 알고리즘

영문 우편번호, 새창, 꽃말, 혈액형, 무한도전, 팝업, 게임, 폰트, 생활의 지혜, 생활의지혜, font, EBS지식채널, 레크레이션, 페이징, 우편번호, 우편번호검색, 셀렉트박스, 아토피, 바베큐, 애드센스,

Today :
Yesterday :

INFOTIP